数学双向理论概述

数学双向理论是一种在数学教育与认知心理学中被广泛讨论的概念。它强调了理解和掌握数学知识的两个重要方面：一方面是对数学概念的理解，另一方面是运用数学技巧解决问题的能力。这两个方面相辅相成，共同构成了学生数学学习的完整过程。

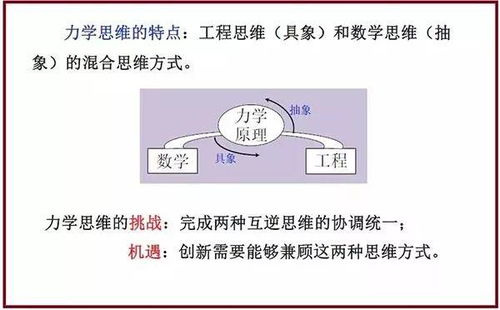
首先，从教学的角度来看，双向理论提倡一种平衡的教学方法，即不仅注重传授数学概念和理论知识，同时也强调实践应用的重要性。这意味着教师在设计课程时需要考虑如何通过实际问题解决来加深学生对数学原理的理解，以及如何利用理论知识去解决生活中的实际问题。例如，在教授几何学时，可以通过让学生设计并建造简单的桥梁模型，来加深他们对形状、空间关系以及结构稳定性的理解。

其次，从学生学习的角度看，双向理论鼓励学生不仅要记住数学公式和定理，还要能够灵活地运用这些知识来分析和解决各种类型的问题。这要求学生具备良好的逻辑思维能力和创造性思考能力。比如，在解决代数问题时，除了直接应用已知的公式外，还需要能够根据问题的具体情况选择合适的解题策略。

再者，从评估的角度来看，双向理论建议采用多元化的评价方式，既包括对数学基础知识掌握程度的测试，也涵盖对实际问题解决能力的考察。这样的评价体系能够更全面地反映学生的数学学习成果，帮助教师更好地了解学生的学习状况，并据此调整教学策略。

最后，从社会需求的角度出发，随着科技的发展和社会的进步，对于具备良好数学素养的人才需求日益增加。双向理论所倡导的教学理念和学习方法，有助于培养出既有扎实数学基础又能灵活运用数学知识解决实际问题的复合型人才，满足现代社会对人才多样化技能的要求。

总之，数学双向理论为我们提供了一种更加全面和有效的数学学习与教学模式。它不仅关注于提高学生的数学知识水平，更重要的是通过理论与实践相结合的方式，激发学生的学习兴趣，提升其解决问题的能力，从而为个人发展和社会进步做出贡献。

• 上一篇：为何村村通卫星电视无法接收信号？寻找解决方案

• 下一篇：打开水管让水流入B处是何感受？